Sensor

Widerstandsthermometer

aus Wikipedia, der freien Enzyklopädie

Wechseln zu: Navigation, Suche

Widerstandsthermometer nutzen die Temperaturabhängigkeit des elektrischen Widerstandes von Leitern aus zur Messung der Temperatur.

Reine Metalle zeigen stärkere Widerstandsänderungen als Legierungen und haben einen relativ konstanten Temperaturkoeffizienten des elektrischen Widerstandes. Für präzise Messungen verwendet man Edelmetalle, meist Platin, da diese besonders wenig Alterung zeigen, und da die Thermometer daraus mit geringen Fehlergrenzen zu fertigen sind. Der Widerstand kann auch aus Keramik (gesinterte Metalloxide) oder Halbleitern bestehen, womit sich sehr viel höhere Temperaturkoeffizienten als mit Metallen und damit auch viel höhere Empfindlichkeiten erzielen lassen, aber mit geringerer Präzision und erheblicher Temperaturabhängigkeit des Temperaturkoeffizienten selber. Man bezeichnet diese Widerstände als Thermistoren, wobei Heißleiter (NTC-Widerstände) in der Messtechnik eher verwendet werden als Kaltleiter (PTC-Widerstände).

Herkömmliche Thermometer messen die Temperatur anhand der Längen- oder Volumenänderung eines Stoffes und sind nur als anzeigende Messgeräte geeignet. Der Vorteil der Widerstandsthermometer liegt darin, dass sie ein elektrisches Signal liefern und sich zum Einsatz in der industriellen Messtechnik eignen, wo sie insbesondere als Platin-Widerstandsthermometer weit verbreitet sind.

Inhaltsverzeichnis

[Bearbeiten] Kenngrößen und Fehlergrenzen

Innerhalb kleiner Temperaturbereiche kann oft die Formel

R_t = R_{20} cdot (1 + alpha_{20} cdot (t - 20;^{circ}mathrm{C}))

angewendet werden. Sind der zur Temperatur t gehörende Widerstand Rt = R(t) , der zu 20 °C gehörende Widerstand R20 und der auf 20 °C bezogene Temperaturkoeffizient α20 (Materialkonstante) bekannt, so kann die Temperatur folgendermaßen berechnet werden:

t = 20;^{circ}mathrm{C} + (R_t / R_{20} - 1)/alpha_{20}

Voraussetzung für eine so einfache Berechnung ist ein eingeengter Messbereich oder ein konstanter Temperaturkoeffizient. Letzteres ist bei Metallen und Silizium nur annähernd der Fall; bei Thermistoren aus Bariumtitanat ist diese Näherung nicht gegeben.

[Bearbeiten] Platin

Für die in der industriellen Messtechnik weit verbreiteten Platin-Messwiderstände gibt es die DIN EN 60751, in der für die Funktion Rt = R(t) hinter dem linearen Glied weitere Summanden angegeben werden

  • für den Bereich t = 0 ... 850 °C R_t=R(t)=R_0;(1+At+Bt^2),
  • für den Bereich t = -200 ... 0 °C R_t=R(t)=R_0; (1+At+Bt^2+C(t-100,^{circ}mathrm{C})t^3)

mit A = 3,9083·10-3 °C-1 ; B = - 5,775·10-7 °C-2 ; C = - 4,183·10-12 °C-4 .

Als Nennwert wird R0 = R(0) angegeben, also der Widerstand bei 0 °C; bevorzugt werden die Nennwerte 100 Ω und 1000 Ω; dann heißen diese Sensoren Pt100 bzw. Pt1000. Die Spanne der Möglichkeiten reicht etwa von Pt10 bis Pt10000. Die in der Tabelle unten enthaltenen Werte sind mit diesen Gleichungen berechnet.

Normalerweise wird Rt gemessen und die Temperatur t gesucht. Die Auflösung ("Umkehrung") dieser Formeln nebst der dazugehörigen Linearisierung ist nicht einfach und wird hier beschrieben.

Thermometer Pt100 müssen in ihren Fehlergrenzen klassifiziert werden.
- Klasse A: Fehlergrenze = 0,15 °C + 0,002 |t| (zulässig bis 650 °C),
- Klasse B: Fehlergrenze = 0,3 °C + 0,005 |t| (das entspricht 0,12 Ω bei 0 °C).

Beispiel zur bevorzugten Klasse B: Bei 500 °C sind Abweichungen des Messwertes zulässig bis ± 2,8 °C.

Der Temperaturkoeffizient des Widerstands wird in der Norm etwas anders als häufig (und auch oben) festgelegt als alpha_0 =frac{Delta R/R_0}{Delta t} , also zur Bezugstemperatur 0 °C statt 20 °C. Der charakterisierende Wert wird aus dem mittleren Temperaturkoeffizienten über die Spanne 0 ... 100 °C berechnet zu α0 = 3,85 · 10-3 °C-1.

[Bearbeiten] Nickel

Nickel besitzt im Vergleich zu Platin eine höhere Empfindlichkeit, es liefert bei gleicher Temperaturänderung eine größere relative Widerstandsänderung. Allerdings ist dieses Material aus der Normung herausgenommen worden. Für Ni100 galt im Bereich von -60 °C bis +180 °C die Gleichung:

R_t=R(t)=100; Omega +At+Bt^2+Ct^4

mit t = Temperatur in °C; A = 0,5485 Ω /°C; B = 0,665·10-3 Ω °C-2; C = 2,805·10-9 Ω °C-4 .

[Bearbeiten] Heißleiter

Heißleiter weisen einen stark nichtlinearen Zusammenhang zwischen Widerstand und Temperatur auf. Zur mathematischen Beschreibung des Verhaltens eignet sich eine Funktion der absoluten Temperatur T in der Form

R_T =R(T) =Acdot e^{frac {B}{T}} =R_{T_0}cdot e^{Bleft( frac{1}{T} -frac{1}{T_0} ight)}

Dabei ist T0 eine beliebige Bezugstemperatur, z. B. 293 K (20 °C). Die Größe B ist eine Material-Konstante; Richtwert B = 2000 ... 6000 K.

Die relativen Fehlergrenzen von R_{T_0} liegen typisch bei 20 %, von B bei 5 %.

Der Temperaturkoeffizient wird hierzu wieder etwas anders definiert und ergibt sich im Grenzfall differenziell kleiner Temperaturänderungen zu

alpha_T =frac{1}{R_T},frac{Delta R}{Delta T} Rightarrow -frac{B}{T^2}

Er verdeutlicht einen mit steigender Temperatur stark abfallenden, aber bei Zimmertemperatur hohen Messeffekt.

Beispiel: B = 3600 K; T = 300 K; αT = - 40 · 10-3 K-1. Das ist gegenüber α0 bei Platin dem Betrage nach rund das Zehnfache.

Durch Zusammenschaltung mit ohmschen Widerständen lassen sich die Probleme der Exemplarstreuungen und der Nichtlinearität vermindern, wodurch allerdings auch die Empfindlichkeit der Messanordnung vermindert wird.

[Bearbeiten] Ausführungen

Platin-Widerstandsthermometer können je nach Ausführung auch bis - 250 °C oder + 1000 °C verwendet werden. Je nach Anwendung befindet sich das Platin in Draht- oder Schichtform auf einem gläsernen oder keramischen Träger und ist für industriellen Einsatz meist von einem Schutzrohr aus korrosions- und hitzefestem Material umhüllt. Bei niedrigeren Temperaturen ist dieses eher ein Metallrohr, bei höheren Temperaturen kommt ebenfalls Keramik zum Einsatz.

Heißleiter können je nach Ausführung z. B. im Bereich 0 … 150 °C verwendet werden. Sie werden in Stab-, Scheiben- oder Perlenform hergestellt, teilweise mit Glas ummantelt.

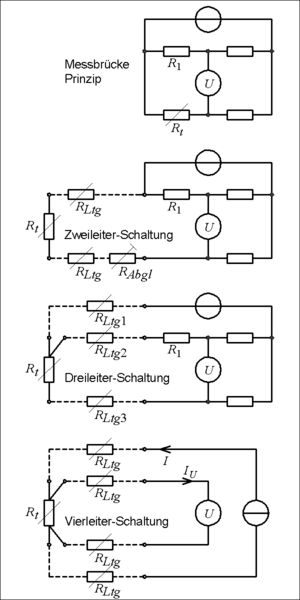
Messschaltungen für Widerstandsthermometer
Messschaltungen für Widerstandsthermometer

[Bearbeiten] Messschaltungen

Zur Widerstandsmessung muss der Widerstand von einem konstanten Strom durchflossen werden. Die anliegende Spannung ist ein leicht messbares, dem Widerstand proportionales Signal. Häufig misst man allerdings nicht diese Spannung, sondern nur ihre Änderung gegenüber einem Anfangswert mittels einer differenz-bildenden Schaltung (Wheatstone-Brücke). Um den Fehler durch Eigenerwärmung gering zu halten, muss der Messstrom möglichst gering sein, beim Pt100 typisch einige Milliampere.

In industriellen Anlagen sind häufig größere Entfernungen zwischen Sensor und Messumformer zu überbrücken mit entsprechend langen Zuleitungen. Um die Einflüsse der Widerstände der Leitungen auf den Messwert zu vermeiden, werden Platin-Widerstandssensoren auch mit Drei- oder Vier-Leiteranschluss gefertigt. Dadurch wird eine getrennte Zuführung des Messstromes möglich bzw. der Zuleitungsfehler kann kompensiert werden. Im Außen-Bereich ist die Installation mit 3 oder 4 Leitern unbedingt anzuraten.

  • Brücken-Schaltung: Für die fast abgeglichene Wheatstone-Brücke (mit kleiner Verstimmung) gilt im Prinzip
    Usim Delta R= R_t-R_1
  • Zweileiterschaltung:
    Usim R_t+2sdot R_{Ltg}+R_{Abgl}-R_1
    Usim R_t+2sdot R_{Ltg}-konst
    Ein ΔRLtg ist nicht unterscheidbar von einem ΔRt . Genormt darf 2sdot R_{Ltg} bis 10 Ω betragen. (Bei kleinerem Leitungswiderstand wird mit einem Abgleichwiderstand auf 10 Ω ergänzt.) Da die Kupfer-Leitungen etwa denselben Temperaturkoeffizienten haben wie ein Pt100, macht sich überschlägig jede Temperatur-Änderung der Leitung bis zu 10 % bemerkbar wie eine Temperatur-Änderung der Messstelle; dabei sind in Freileitungen Schwankungen um 50 … 70 °C realistisch.
  • Dreileiter-Schaltung:
    Usim (R_t+ R_{Ltg3})-(R_1 +R_{Ltg2})
    Usim R_t-R_1 .
    Bei gleichen Leitungen fällt RLtg heraus. (Ein Abgleichwiderstand ist dann überflüssig.) RLtg1 wirkt wie ein Quellenwiderstand der Speisespannung und macht sich praktisch nicht bemerkbar.
  • Vierleiter-Schaltung: Mit einer elektronisch stabilisierten Konstantstromquelle ist I unabhängig von Rt und von RLtg in den Speiseleitungen. Wenn man einen elektronischen Spannungsmesser mit hohem Eingangswiderstand verwendet, wird I_Ull I (keine merkliche Stromverzweigung) und I_U sdot R_{Ltg}ll Isdot R_t (kein merklicher Spannungsverlust in den Messleitungen), so dass U=Isdot R_t wird, also Usim R_t .

[Bearbeiten] Tabelle

Werte für verschiedene gängige Widerstandsthermometer
Temperatur
in °C		 Pt100
in Ω		 Pt1000
in Ω		 PTC
in Ω		 NTC
in Ω		 NTC
in Ω		 NTC
in Ω		 NTC
in Ω		 NTC
in Ω
Typ: 404 Typ: 501 Typ: 201 Typ: 101 Typ: 102 Typ: 103 Typ: 104 Typ: 105
−50 80,31 803,1 1032
−45 82,29 822,9 1084
−40 84,27 842,7 1135 50475
−35 86,25 862,5 1191 36405
−30 88,22 882,2 1246 26550
−25 90,19 901,9 1306 26083 19560
−20 92,16 921,6 1366 19414 14560
−15 94,12 941,2 1430 14596 10943
−10 96,09 960,9 1493 11066 8299
−5 98,04 980,4 1561 31389 8466
0 100,00 1000,0 1628 23868 6536
5 101,95 1019,5 1700 18299 5078
10 103,90 1039,0 1771 14130 3986
15 105,85 1058,5 1847 10998
20 107,79 1077,9 1922 8618
25 109,73 1097,3 2000 6800 15000
30 111,67 1116,7 2080 5401 11933
35 113,61 1136,1 2162 4317 9522
40 115,54 1155,4 2244 3471 7657
45 117,47 1174,7 2330 6194
50 119,40 1194,0 2415 5039
55 121,32 1213,2 2505 4299 27475
60 123,24 1232,4 2595 3756 22590
65 125,16 1251,6 2689 18668
70 127,07 1270,7 2782 15052
75 128,98 1289,8 2880 12932
80 130,89 1308,9 2977 10837
85 132,80 1328,0 3079 9121
90 134,70 1347,0 3180 7708
95 136,60 1366,0 3285 6539
100 138,50 1385,0 3390
105 140,39 1403,9
110 142,29 1422,9
150 157,31 1573,1
200 175,84 1758,4
dient dem Zeilenumbruch, bitte nicht entfernen


[Bearbeiten] Weblinks

Copyright © 2005-2010 Hardware-Aktuell. Alle Rechte vorbehalten.