Sensor

Feldplatte

aus Wikipedia, der freien Enzyklopädie

Wechseln zu: Navigation, Suche

Feldplatten (auch: MDR, Magnetic Dependent Resistor) sind Halbleitersensoren, die auf Magnetfelder reagieren, indem ihr Widerstand ansteigt. (Siehe auch Hallsonde)

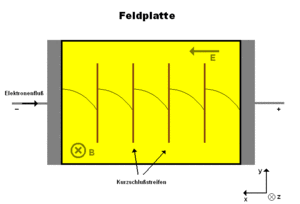
Sie bestehen aus Indiumantimonid (InSb), das eine hohe Elektronenbeweglichkeit besitzt. Während der Herstellung werden in das Material Kurzschlussbrücken aus Nickelantimonid (NiSb) eingebracht. NiSb hat eine wesentlich höhere Leitfähigkeit als InSb und dient dazu, die Elektronen homogen zu verteilen bevor sie in den nächsten Plattenabschnitt gelangen. Sie würden sich sonst auf einer Seite anlagern.

Wenn an der Feldplatte kein Magnetfeld wirkt, so liegt ein definierter Grundwiderstand vor, die Elektronen durchqueren die Platte entsprechend geradlinig. Wirkt nun von außen ein Magnetfeld ein, so werden die Elektronen abgelenkt und es kommt zu einer Wegverlängerung und damit zu einer Widerstandserhöhung.

Diese Erhöhung kann als Signal genutzt werden um z. B. die Stärke des Magnetfeldes zu bestimmen, als Näherungsschalter oder – mit Polrad – als Drehzahlmesser.

Feldplatten werden zunehmend durch AMR- oder GMR-Sensoren ersetzt, da diese vor allem höhere Betriebstemperaturen und bessere Linearität aufweisen. Feldplatten sind daher kaum noch serienmäßig erhältlich und in den meisten Bauformen obsolet.

[Bearbeiten] Herleitung der Widerstandserhöhung

Die Kraft die auf eine Ladung wirkt, wenn diese elektromagnetische Felder durchquert, ist gegeben durch die Lorentzkraft:

vec F=q cdot left(vec E + vec v times vec B right)

Für Halbleiter gilt wie auch bei Metallen das Ohmsches Gesetz, hier in seiner mikroskopischen Formulierung:

vec j=sigma cdot vec E

Hierbei ist vec j die Stromdichte, σ die Leitfähigkeit und vec E die elektrische Feldstärke. Hierbei ist die elektrische Feldstärke gleich der an der Feldplatte anliegenden Spannung.

Die Leitfähigkeit kann so dargestellt werden:

sigma=q cdot n cdot mu=rho cdot mu

Dabei ist q die Ladung der Teilchen, n die Teilchendichte (auch Teilchenverteilung), μ die Beweglichkeit der Teilchen und ρ ist somit die Ladungsdichte (oder Ladungsverteilung).

Dadurch wird das Ohmsches Gesetz umgeformt zu:

frac{vec j}{rho}=mu cdot vec E quad Rightarrow quad vec v=mu cdot vec E qquad , denn vec j:=rho cdot vec v

Das Ergebnis ist die Driftgeschwindigkeit der Teilchen.

Mit vec F=q cdot vec E, die auf eine Ladung aufgrund eines Feldes wirkende Kraft, wird die Driftgeschwindigkeit umgeformt zu:

vec v=mu cdot frac{vec F}{q}

Eigentlich ist bei Halbleitern der fließende Strom gegeben aus der Summe über Elektronestrom und Löcherstrom. Da die Halbleiter für Feldplatten (oft InSb) nur für einen der Ladungsträger eine hohe Beweglichkeit haben, kann der jeweils andere Strom vernachlässigt werden. So hat InSb eine etwa 70 mal bessere Beweglichkeit für Elektronen:

vec j=vec j_n+vec j_p approx vec j_n quad, mu_n gg mu_p


Gehen wir nun davon aus, die Platte läge in der x-y-Ebene (sie ist also dünn), das E-Feld sei in Richtung der x-Achse und das B-Feld (genauer gesagt die magnetische Induktion) in Richtung der z-Achse.

Daraus folgt für die Lorentzkraft:

vec F=q cdot left[ begin{pmatrix} E_x 0 0 end{pmatrix} + begin{pmatrix} v_x v_y 0 end{pmatrix} times begin{pmatrix} 0 0 B_z end{pmatrix} right]=q cdot begin{pmatrix} E+v_yB -v_xB 0 end{pmatrix} qquad, vertvec Evert=E_x=E, vertvec Bvert=B_z=B, vertvec vvert=sqrt{v_x^2 + v_y^2}

Setzt man das in die Gleichung für die Driftgeschwindigkeit ein, so folgt:

begin{pmatrix} v_x v_y end{pmatrix}=mu begin{pmatrix} E+v_yB -v_xB end{pmatrix} quad Rightarrow quad v_x=mu E - v_x mu^2 B^2 quad Leftrightarrow quad v_x=frac{ mu E}{1+left(mu Bright)^2}

Der Widerstand der Platte hängt sicherlich nur von dem Strom in Richtung des E-Feldes ab (jx = ρvx), daher ist auch nur die Geschwindigkeit in dieser Richtung interessant. Diese nimmt bei steigendem B-Feld ab, wie man sieht.

Wird die Geschwindigkeit der Ladungsträger verkleinert, so muss sich der Stromfluss verkleinern:

v_x rightarrow frac{v_x}{alpha} quad Rightarrow quad j_x rightarrow frac{j_x}{alpha} quad Rightarrow quad sigma rightarrow frac{sigma}{alpha} qquad, vec j=rho cdot vec v, quad vec j=sigma cdot vec E

Verkleinert sich der Stromfluss, so muss sich bei gleichgebliebenem E-Feld (Spannung) die Leitfähigkeit verkleinert haben.

Da der Widerstand inverse Leitfähigkeit ist, stiegt bei kleinerer Leitfähigkeit der Widerstand:

sigma rightarrow frac{sigma}{alpha} quad Rightarrow quad R rightarrow Ralpha qquad,R=sigma^{-1}

Das heißt der Widerstand der Feldplatte vergrößert sich bei steigendem B-Feld folgendermaßen:

R(B)=R_0 left( 1+left(mu Bright)^2 right)

[Bearbeiten] Siehe auch

[Bearbeiten] Weblinks

Copyright © 2005-2010 Hardware-Aktuell. Alle Rechte vorbehalten.